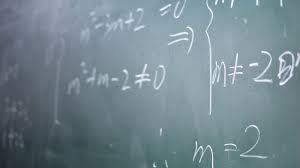Students often find math equations challenging because they don’t know how to use them or where to use them. Math equations are not just for memorizing for a math examination; students can enjoy them using an equation solver.
Equations are a lot more than deep educational knowledge; it is art in itself. Just like the AMC math competition or other math tournaments, science and art meld. Students can enjoy comprehending and applying equations in different aspects of life.
Here is a compiled list of startling, unique, insane equations that serve more than their original purpose:
Table of Contents
Euler’s Identity
A well-known equation, Euler’s identity, is related to the random values of pi and also the square root -1. Most people regardsEuler’s identity as the most beautiful mathematics equation.
e ix = cos x+ i sin x
A simplified formula is
If x=π, the value of cos x is -1, while i sin x is 0, it results in Euler’s identity as -1+1=0
The Gaussian Integral
The Gaussian Integral is a terrible function to assimilate when trying to do it in a real line or a line beginning from minus infinity and continuing up to infinity. You may use an online equation solver to assimilate in the real line.
At first glance, you won’t be able to notice that the area under the curve is actually the square root of pi. However, this formula,e-x2 to the power of minus x square, is highly important in statistics as it characterizes the normal distribution.
The Cardinality of the Continuum
George Cantor states, the father of set theory, first showed the cardinality of a real number. It states cardinality of a real number or any number, to be precise, is equal to the cardinality of the subset of the number.
According to the cardinality of the continuum, a continuum is uncountable as two to the power of n is more significant than n.
The continuum hypothesis states that there is no cardinal number between N and R. Strangely, the property of the continuum is that it can neither be proved nor can be disapproved. Use an equation solver with steps to understand the concept better.
The Analytic Continuation of the Factorial
The easiest way to define a factorial is by stating it as n! = n(n-1)(n-2)….1. However, this equation has a drawback; it works only for positive integers.
However, the integers could be in any form; fractions or decimal. If you want to use the analytic continuation of factorial in negative integers, you will have to call it a different name, the gamma function.
The Pythagorean Theorem
One of the most common yet most amazing equations is the Pythagoras theorem. It says that if a and b are the lengths of the legs of a right-angled triangle, the length of the hypotenuse is equal to the squares of the sides.
Or, a2 + b2 = c2. If you still cannot understand what the theory means, take the help of an equation solver calculator to make your work easy.
The above-mentioned equations describe quite easily students can use them and apply them using the simple equation.
Additional Reads-
How to Find the Surface Area and Volume of a Cube?
CDR Help To Pass The Migration Skill Assessment With Ease.